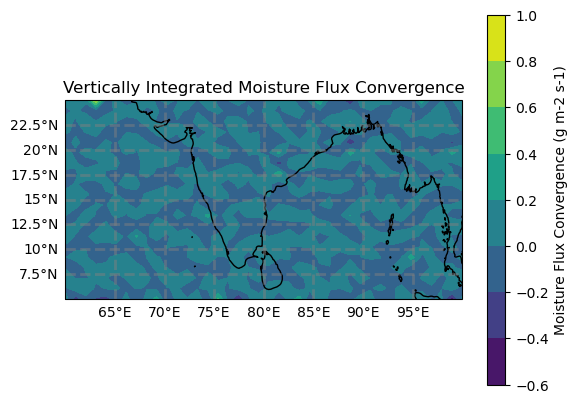
Vertically Integrated Moisture Flux Convergence#
This script illustrates calculating vertically integrated moisture flux convergence (MFC) for a dataset with a constant pressure level system.
To calculate this, we must first leverage geocat.comp.meteorology.delta_pressure for the vertical integration, and then geocat.comp.gradient.gradient to get our gradients on the surface of the WGS84 ellipsoid.
import xarray as xr
import numpy as np
import geocat.comp as gc
import geocat.datafiles as gcd
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
Load Data#
Here we load in a dummy Xarray Dataset with 2d zonal and meridional wind componenets (u_wind and v_wind), 3d water vapor (q_vapor), a 2d surface pressure array (surface_pressure), and a 1d pressure level system (pressure_lev).
ds = xr.open_dataset(gcd.get("netcdf_files/dummy_uvqp_data.nc"))
ds
<xarray.Dataset>
Dimensions: (x: 20, y: 40, lev: 13)
Coordinates:
lon (x, y) float64 ...
lat (x, y) float64 ...
pressure_lev (lev) int64 ...
Dimensions without coordinates: x, y, lev
Data variables:
u_wind (x, y) float64 ...
v_wind (x, y) float64 ...
q_vapor (x, y, lev) float64 ...
surface_pressure (x, y) float64 ...Vertical Integration#
To do a mass-weighted vertical integration of our 3d water vapor, we need to first get a layer mass weighting. This is our delta pressure levels, divide by the gravitational constant. Then, multiply the layer mass weighting by the water vapor variable, and integrate vertially.
delta_pressure_levels = gc.meteorology.delta_pressure(pressure_lev=ds.pressure_lev, surface_pressure=ds.surface_pressure)
g = 9.80665 # gravitational acceleration (m s-2)
layer_mass_weighting = delta_pressure_levels / g # Layer Mass Weighting
layer_mass_weighting .attrs["units"] = "kg m-2"
mass_weighted_vapor = ds.q_vapor * layer_mass_weighting # mass weighted 'q'
iq = mass_weighted_vapor.sum(dim="lev") # Vertically Integrated Vapor
iq.attrs["units"] = "g m-2"
Calculate Moisture Flux Convergence (MFC)#
The formula for MFC is as follows:
\(MFC = -u\frac{dq}{dx} - v\frac{dq}{dy} - q\left(\frac{du}{dx} + \frac{dv}{dy}\right)\)
where u represents the zonal wind component, v is the meridional wind componenet, and q is the moisture content (in our case, vertically integrated).
Sure! Here’s how you can fix the equations in the line of text:
The first two terms of this equation, \(-u*\frac{dq}{dx} - v*\frac{dq}{dy}\), are together the advection term, and the last term, \(q(\frac{du}{dx} + \frac{dv}{dy})\), is our convergence term, with moisture flux convergence being the advection minus the convergence.
Source: Banacos and Schultz, “Moisture Flux Convergence”, NOAA 2004
To do this calculation, we first need the gradients of our wind components and moisture. We are using Geocat-comp’s gradient method because of its improved accuracy for geospatial data over an Earth-like ellipsoid.
du_dx, du_dy = gc.gradient(ds.u_wind) # (s-1)
dv_dx, dv_dy = gc.gradient(ds.v_wind)
dq_dx, dq_dy = gc.gradient(iq) # (g m-3)
advection = (-ds.u_wind * dq_dx) - (ds.v_wind * dq_dy) # (g s-1 m-2)
convergence = iq * np.add(du_dx, dv_dy) # (g s-1 m-2)
mfc = advection - convergence # moisture flux convergence (g m-2 s-1)
mfc
<xarray.DataArray (x: 20, y: 40)>
array([[ 1.22064703e-01, -3.12128939e-01, -5.96595436e-02,
-2.25516841e-01, -2.70725319e-01, -1.20396395e-01,
7.55133505e-02, -2.09545354e-01, 8.72083656e-02,
2.61595018e-01, -2.06763083e-01, 7.83812372e-02,
2.05628902e-02, 1.43312631e-01, -2.37694081e-01,
4.22776599e-01, -5.96577422e-02, -4.16869163e-01,
-1.14914013e-02, 1.00259343e-01, 1.61890966e-01,
-2.60197367e-01, 8.82344837e-02, 3.03994766e-01,
-1.40376617e-01, 1.20312225e-01, -5.02249982e-02,
-7.68566796e-02, -5.46356546e-02, 7.02835463e-02,
4.93524082e-02, -9.00835117e-02, -5.58480753e-02,
8.14280214e-02, 3.55652926e-02, 1.42111460e-01,
-1.01098113e-02, 1.81838364e-02, -5.45783703e-01,
5.91513590e-02],
[-3.12641494e-02, 1.06947688e-01, 1.34283405e-01,
-3.37847424e-02, 1.08115689e-02, 2.52913528e-02,
-4.24634114e-02, 1.14821632e-02, -1.25382538e-02,
-4.01496953e-02, -1.60356749e-02, 3.74027805e-02,
-1.98496909e-01, -7.18312195e-03, 3.60838236e-02,
1.96114748e-02, -1.36222200e-02, 6.11933885e-02,
...
-6.05720215e-02, -1.36193152e-02, -6.09674563e-02,
-3.29536498e-02, 5.78628885e-02, -6.48545969e-02,
-7.21760370e-04, -4.87134738e-02, -1.86083236e-02,
5.85945369e-02, 1.13874248e-02, -1.43162411e-01,
-2.02898566e-04, 2.79319413e-02, -1.66124378e-02,
5.51563881e-03],
[ 5.55114858e-02, 1.68997453e-01, 1.66522592e-02,
8.01187703e-01, -3.32522823e-02, 1.91175311e-02,
-7.35270175e-02, -1.13793947e-02, 5.80357475e-02,
-2.23158586e-02, 3.34206763e-02, -1.39950975e-02,
1.29816405e-01, -2.35926059e-02, 1.44941552e-01,
-4.50552110e-02, -1.06261601e-02, 1.61398009e-01,
-2.80416590e-02, -2.91196876e-02, 1.15526957e-02,
1.93081846e-02, 1.20017887e-01, -1.00753797e-01,
1.20826703e-02, 3.44358041e-01, -7.73621468e-02,
-4.84163671e-02, -4.34982935e-01, 1.04188116e-01,
1.88039124e-02, 3.11744643e-02, 1.12264981e-02,
-9.14767360e-02, -2.43382261e-01, 3.13623859e-01,
-1.19396210e-01, 5.60148017e-04, -9.61885753e-03,
1.24913746e-01]])
Coordinates:
lon (x, y) float64 60.0 61.03 62.05 63.08 ... 96.92 97.95 98.97 100.0
lat (x, y) float64 5.0 5.0 5.0 5.0 5.0 5.0 ... 25.0 25.0 25.0 25.0 25.0
Dimensions without coordinates: x, yPlot Data#
And finally we can view our moisture flux convergence.
ax = plt.axes(projection=ccrs.PlateCarree())
plt.contourf(ds.lon, ds.lat, mfc, transform=ccrs.PlateCarree())
plt.title('Vertically Integrated Moisture Flux Convergence')
ax.set_xlabel('Longitude')
ax.set_ylabel('Latitude')
cbar = plt.colorbar()
cbar.set_label('Moisture Flux Convergence (g m-2 s-1)')
ax.coastlines()
gl = ax.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.top_labels = False
gl.right_labels = False;
/Users/jkent/miniconda3/envs/gc-docs/lib/python3.10/site-packages/shapely/predicates.py:798: RuntimeWarning: invalid value encountered in intersects
return lib.intersects(a, b, **kwargs)